Abstract
There are a LOT of algorithms for recommender systems. In this post, I will try to list a part of them (and hopefully a large part). I will not introduce what are
recommender system, what they are for, etc ... I have a post that
introduce the concept a little, but the goal here is to go straight to the point. Thus I will present each algorithm in few lines in order to just to have the big
picture of each algorithm is solving and what they model. In a second part of this post, I'll try to compared them on different
datasets and give the code on my github, but this will be a very painful work !
I'll try to have a dozen of algorithm codes before moving to experiments parts.
There are :
- 11 algorithms named so far
- 5 algorithms detailed so far
- 0 algorithms tested experimentaly so far
- 5 codes available
Presentation of the algorithms
Contextual Matrix Factorization
- [Display] -
Most of the time matrix factorization for recommencer system is apply on the user x item feedback sparse matrix thus without any contextual knowledge on the user or the item.
This is often sufficient because the implicit description obtained from the rating of a user is less bias than an explicit description like age, gender, ... . But when a
user is new to the system (cold start problem), the implicit description won't be enough to make proper recommendation.
Some hybrid methods are then derived by computing a weighted average between a collaborative filtering (CF) algorithm (rely only on the feedback) and
acontent-based methods (rely on the context). But those methods are not really satisfactory since it need to manualy tune to weight of the average.
A better way to do so is to add extra column and extra row to the CF matrix and filling them with the context. For instance, let R be the sparse CF matrix scaled
between 0 and 1 (that is if we add before 1 to 5 stars for a rating it is now 0.2 to 1), where each line
is a user and each column a movie. For each user we know if it's a male or a female, and it's age. Let's dummify everithing : so we add a first column that worth 1 if the
user is a male, 0 otherwise, a second column for female, a third if the user have less than 10 years old, a fourth between 10 and 20 years old, etc ... Likewise we add a
first row if the movie is an action movie, a second row for thriller, ... a nth for the actor being 'some actor' ... We end up with a bigger matrix that look like this :
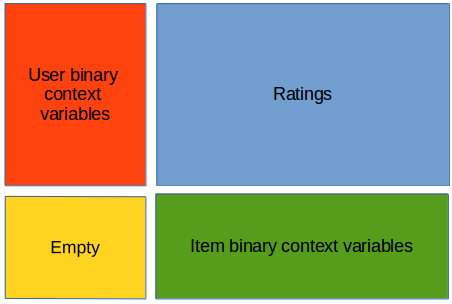
We can then apply any matrix factorization techniques we want, like ALS-WR, RSVD, etc that we will see just below. The nice things is that the weight between context and
ratings in the feature description will be automatic : if the user have only 2 ratings, and we have 10 context informations, most of the weight will be in the context; if
the user have 50 ratings, the weight will be in the ratings. Finally, when filling the empty matrix by learning, we obtained context x context taste like what kind of movie
young people prefer, which can be an interesting insight. In the experiments section I will learn the model
in pure CF and with context and will refer to this model by "context_method" like "context_ALSWR".
Of course there are other techniques like Factorization Machines that we will see below too, but I think it is interesting to compare Factorization Machines with
contextual matrix factorization instead of with pure collaborative filtering for fairness issues !

ALS-WR : Alternating-Least-Squares with Weighted-λ-Regularization
- [Display] -
[Source]
Algorithm

- $R \in \mathbb{R}^{ n \times p} = (r_{ij})$ denote the sparse user-item matrix.
- $\mathcal{D}$ is the set of available ratings.
- Assume a low rank constraint $K$ on the matrix : $R = UV^T$, $U,V \in \mathbb{R}^{ n \times K}, \mathbb{R}^{ p \times K}$
- $U_i$ and $V_j$ denotes respectively the latent features of user $i$ and item $j$.
- $n^{\mathcal{U}}_i$ is the number of ratings provided by user $i$.
- $n^{\mathcal{I}}_j$ is the number of ratings available for item $j$.
- $\mathcal{I}_i$ and $L\mathcal{U}_j$ is respectively the set of rated item by user $i$ and available ratings for item $j$.
- $\hat{r}_{ij} = U_iV_j^T$

RSVD: Regularized SVD
- [Display] -
[Source]
Algorithm

- Very close to ALS-WR but little change on the regularization and learning is done by stochastic gradient descent
- $\hat{r}_{ij} = U_iV_j^T$
- $lrate$ is the learning rate of the SGD

imp RSVD: Improved Regularized SVD
- [Display] -
[Source]
Algorithm

- Add a user bias $c_i$ and an item bias $d_j$
- $\hat{r}_{ij} = c_i + d_j + U_iV_j^T$
- $lrate$ is the learning rate of the SGD

FM : Factorization Machines
- [Display] -
[Source]
Algorithm

- Training set $S = \{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots \}$
- $x^{(i)} \in \mathbb{R}^n$ is a sparse vector represent all the context (user, item, time, ...). For instance the $m$ first values is a dummy variable indicating which user is it, the next $p$ is a dummy variable for the item, then the month, the moment of the day, the last seen item, ...
- $y^{(i)}$ is the rating
- Model equation of a machine of degree 2: $\hat{y}(x) = w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n < v_i, v_j > x_i x_j$
- $w_0 \in \mathbb{R}$, $w \in \mathbb{R}^n$, $V \in \mathbb{R}^{n \times k}$
- $< v_i, v_j > = \sum_{f=1}^k v_{i,f} v_{j,f}$
- With the right input, FM can mimic several other alogrithms (Matrix Factorization, SVD++, ...)
- $\Theta = {w_0, w, V}$

RBM for CF : Restricted Boltzmann Machine for Collaborative Filtering
- [Display] -
[Source]
Algorithm

Make a prediction
We have for a given user $u$ and his corresponding matrix $V$:
$$p(v_{q,k}=1|V) \propto \Gamma_q^k \prod_{j=1}^F \left( 1+\exp(\sum_{il}v_{i,l} W_{l,i,j} + v_{q,k} W_{k,q,j} + {V_b}_j) \right)$$
We then output the value by taking the weighted average :
$$R_{u,q} = \frac{\sum_k k p(v_{q,k}=1|V)}{\sum_k p(v_{q,k}=1|V)}$$
- It's a RBM !, but ...
- We learn a RBM per user
- All weights and biases are tied accross all users by averaging the gradient over all users
- For a partular RBM, so a particular, there is only has many visible units as the user had rated items, but always the same number of hidden units
- Each RBM have only a single training example. It is the vector of ratings amoung previously rated items
- Each visible unit is a softmax unit of size K if an item can be rated between 1 and K.
- The visible unit is a matrix $V \in \mathbb{R}^{m \times K}$ where $m$ is the number of item rated by the user, and $V_{i,k}=1$ is the user give a rate of $k$ to movie $i$ and $0$ otherwise.

SVD++
- [Display] -
[TBD]
Algorithm

- Very close to impRSVD but with an extra term introducing "implicit" feedback that are previously rated movie by the user (regardless the rating)
- $\mu$ global bias
- $y_j$ extra set of item factors characterizing users based on the set of items they rated
- $R(u)$ contains the items rated by user u
- $\hat{r}_{ij} = \mu+c_i+d_j+V_j^T(U_i+|R(i)|^{-1/2} \sum_{p \in R(i)} y_p)$
